Um ‘teste de DNA’ para planetas
Em 2006, a União Astronômica Internacional causou rebuliço mundial ao criar, pela primeira vez, uma definição oficial do que é um planeta. A iniciativa levou ao rebaixamento de Plutão e criou um racha — ainda não totalmente resolvido — entre cientistas planetários e astrônomos. Mas agora um pesquisador da Universidade da Califórnia em Los Angeles criou um método matemático rigoroso para verificar prontamente se qualquer objeto — esteja ele no Sistema Solar ou não — se enquadra na classificação original da IAU. É praticamente um “teste de DNA” para planetas. E Plutão, como era de se esperar, não passa nele.

O trabalho foi apresentado na semana passada, durante a reunião anual da Divisão de Ciências Planetárias da Sociedade Astronômica Americana, e representa um possível refinamento da definição original da IAU, que permite inclusive sua aplicação imediata aos planetas descobertos fora do Sistema Solar. Esse, aliás, é um ponto importante. Em sua definição original, de 2006, a “Fifa da astronomia” especificou que a definição de planeta se aplicava somente aos planetas solares, deixando para um momento futuro a ampliação do conceito para outros sistemas planetários.
O que Jean-Luc Margot propõe é uma definição matemática rigorosa de planeta, que se sobrepõe exatamente à proposta original da IAU, e que pode ser testada usando apenas os parâmetros facilmente determináveis dos exoplanetas — basicamente massa da estrela, período orbital e massa do planeta.
O QUE É UM PLANETA?
De acordo com a IAU, para entrar na categoria de planeta, um corpo celeste precisa atender três critérios. O primeiro e mais elementar é estar em órbita do Sol (ou de uma estrela qualquer, se quisermos estender o conceito aos exoplanetas).
O segundo é ter massa e composição tais que o corpo seria capaz de entrar em equilíbrio hidrostático — ou, falando em português claro, tenha assumido a forma aproximadamente esférica.
Finalmente, o terceiro — e controverso — critério é que o corpo tenha “limpado” a região de sua órbita, o que é genericamente interpretado como a dominância do objeto ao longo de seu trajeto. Foi aí que Plutão caiu — como sua órbita está na mesma região de grande quantidade de objetos, alguns deles do mesmo tamanho que ele, no cinturão de Kuiper, não se pode argumentar que ele “limpou” sua órbita.
Curiosamente, a órbita de Plutão também intersecta a de Netuno, que é tido como planeta. E aí? Bem, a verdade — apontada também por Margot em seu trabalho — é que nenhum corpo pode existir de forma completamente isolada em sua órbita. Mesmo a Terra tem sua órbita cortada por vários asteroides — motivo pelo qual corremos o risco de um impacto, mais dia, menos dia. Daí a noção de dominância, sem exigir uma limpeza absolutamente completa. Nesse caso, Netuno claramente é dominante. Aliás, Plutão só está ali, porque está numa órbita “coordenada” com Netuno, em que, a cada duas voltas do primeiro, o outro completa exatamente três, de forma que ambos nunca se encontram no mesmo lugar do espaço.
O problema é: como quantificar de forma exata a tal “dominância”? É isso que o astrônomo da Califórnia propõe resolver. Jean-Luc Margot sugere colocar a questão em outros termos, definindo dominância como a capacidade de um corpo celeste de ejetar objetos menores de sua faixa orbital ao longo de um período arbitrário, possivelmente o tempo estimado de vida de sua estrela-mãe. A faixa orbital é definida por ele como 3,5 ou 5 vezes o chamado raio de Hill. A esfera de Hill é basicamente a região em que o campo gravitacional de um astro é capaz de manter satélites. No caso da Terra, a esfera de Hill tem cerca de 1,5 milhão de km de raio. Ou seja, mesmo na definição mais “frouxa” proposta por Margot, a região a ser limpa é considerável, algo como uma faixa de mais de 10 milhões de km ao longo da órbita.
Em seu trabalho, aceito para publicação no “Astronomical Journal”, ele aplica essa fórmula para os planetas do Sistema Solar, e o resultado está muito alinhado com a definição original da IAU. De um lado, claramente caem os oito planetas aceitos — Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano e Netuno. Do outro, com grande distância, caem os planetas anões Ceres, Plutão e Éris. Veja o gráfico abaixo.
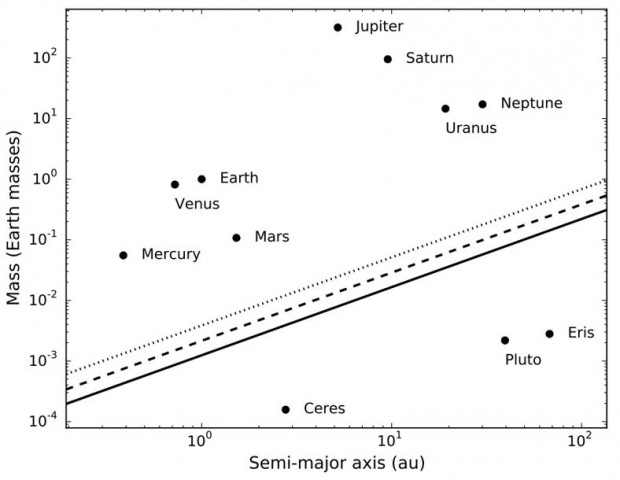
“A disparidade entre planetas e não-planetas é chocante”, disse Margot, em nota. “A distinção clara sugere que existe uma diferença fundamental em como esses corpos se formaram, e o mero ato de classificá-los revela algo profundo sobre a natureza.”
Ou, em outras palavras, a IAU parece mesmo ter feito a coisa certa em dividir os objetos aproximadamente esféricos em torno do Sol em planetas e planetas anões. (Sorry, Plutão!)
EXOPLANETAS
Além de confirmar a sabedoria da definição da IAU, o trabalho de Margot também oferece o caminho para expandi-la para outros sistemas planetários. Ao definir matematicamente a capacidade de “limpar a órbita” e usar como parâmetro o tempo de vida da estrela, sua equação-teste pode ser aplicada a praticamente qualquer dos sistemas já descobertos.
Isso porque tudo que ela pede é a massa da estrela (que permite derivar o tempo de vida), a massa do planeta (que nem sempre é determinada, mas pode ser estimada com base no diâmetro, que é o parâmetro calculável nos planetas descobertos pelo método do trânsito) e a órbita do planeta (derivada a partir do período).
Aplicando sua fórmula aos exoplanetas já descobertos, Margot constatou que é capaz de confirmar que 99% deles são de fato planetas — evidência de que a estratégia é útil e não dependerá de nossa capacidade de obter mais informações sobre esses mundos para classificá-los.
Ainda não sabemos se a proposta de Margot — ou alguma outra parecida — será incorporada pela IAU à sua definição, quando chegar a hora de expandi-la para englobar outros sistemas planetários. Mas sem dúvida parece ser a coisa certa a fazer.

Bom, tenho que render ao fato de que Plutão não é planeta…
Acho, porém, que é – como o Salvador disse uma vez – que Plutão é um “objeto” pra lá de interessantíssimo!
🙂
P.S. Acho, porém, o termo “planeta anão” horrível. Deveria ser “planeta deficiente em dimensões e massa”. Ou ter um nome mais adequado, diferente.
Exato! Titã, Europa e Encélado com certeza não são plaanetas, mas são incríveis!!! 🙂
Salvador, por favor me corrija se eu estiver errado: o gráfico apresentado relaciona apenas a massa do planeta (eixo vertical) com o raio da sua órbita (eixo horizontal). Não entendi onde entra a “esfera de Hill” no gráfico. De acordo com esse gráfico, planetas são aqueles corpos cuja massa é grande em relação ao raio da sua órbita.
Complementando: se acordo com o gráfico, para ser classificado como planeta, o critério é que quanto mais afastado da estrela, mais massivo o corpo precisa ser.
Leia a legenda para ver onde entra a esfera de Hill! A linha divisória é traçada de acordo com o tempo mínimo levado em conta (4,6 bi de anos ou 10 bi de anos) e da área orbital a ser limpa (3,5 ou 5 raios de Hill).
O interessante é que o critério quantitativo tenha sido apresentado nos EUA por um professor da UCLA. Os americanos foram os que mais fizeram oposição à “degradação” de Plutão em 2006. O motivo era, provavelmente, muito sentimental, Plutão é o único planeta “americano”. Detalhe a se ter em conta, J-L Margot é de origem belga. A ciência também é cheia dessas briguinhas.
Salvador, andei lendo uns posts mais antigos e vi vc dizendo que a gravidade dos corpos se estende por todo o universo, em tese. Isso me faz lembrar aquele exemplo de imaginar um lençol estendido com uma bola de futebol no meio, a depressão causada sendo efeito da gravidade. Agora conta pra gente como veríamos esse mesmo lençol se pudéssemos ter uma “visão especial” e enxergasse o espaço-tempo curvado a nossa volta em tempo real? HEHE
Rapaz, é difícil de imaginar o tal lençol sem sacrificar uma das três dimensões que vemos na representação da curvatura. A imagem do lençol só funciona porque ele tem duas dimensões. Mas não conseguimos visualizar a curvatura em três dimensões…
Caro Salvador, Parabéns pela coluna. Sou um assíduo devorador de seus artigos.
Como principiante gostaria de expandir a visão do lençol, isto se possível.
Consideremos não um lençol, mas uma piscina com um objeto mergulhado em seu centro. Este objeto sendo um ponto de alta gravidade. Isto faria aparecer as curvas em 3D?
Considerando o produto espaço tempo constante, uma vez que tenhamos as curvas de espaço se projetando para o centro do ponto de alta gravidade, teríamos as curvas de tempo de afastando do mesmo ponto na mesma proporção?
Não, porque para ver a curva em 3D você teria de enxergar uma quarta dimensão representando a curvatura — e isso nós, pobres humanos, não temos como fazer. Só conseguimos representar dimensões extra de forma matemática, mas não podemos visualizá-las (porque vivemos e evoluímos para enxergar três dimensões espaciais!).
Interessante, embora a deformação do espaço-tempo ao redor do corpo rodeie todo seu entorno, como na imagem 3D a seguir, não consegui, de fato, vislumbrar nela a curvatura do tecido espaço tempo.
http://2.bp.blogspot.com/-qlv_BR-XqAs/VdSMbZ6hwYI/AAAAAAAACJY/gtSXwKqCQfM/s1600/espa%25C3%25A7o-tempo-3d.jpg
O Salvador, tem toda a razão, essa representação só faz sentido em 2D, como no exemplo do lençol entendido.
Para complicar ainda mais, dizem que o espaço-tempo é uma realidade quadridimensional, só que essa representação só pode ser observada por meio de números de equações matemáticas que dão suporte a teoria da relatividade.
Não contestando o requisito de que um planeta deve ser capaz de limpar a sua órbita, mateticamente, é possível que possam haver planetas co-orbitantes ao redor de uma estrela, ou seja, planetas que dividem uma mesma órbita, basta que outro planeta ocupe pontos específicos ao redor da órbita, pontos esses conhecidos como pontos de Lagrange.
Tal ocorrência pode ser vista em sistemas estrelares ainda jovens. Ou seja, os planetas não tiveram tempo de limpar as suas órbitas.
O telescópio espacial Kepler descobriu em 2011 dois planetas que compartilham a mesma órbita. Esse arranjo orbital, contudo, deve se desgrilhoar daqui há alguns milhões de anos e os planetas co-orbitantes devem vir a se chocar, repetindo o mesmo tipo de cataclisma que, em tese, deu origem a nossa Lua.
http://eternosaprendizes.com/2011/02/28/koi-730-astronomos-descobrem-em-dados-do-kepler-um-par-de-exoplanetas-que-residem-na-mesma-orbita-da-sua-estrela/
Victor, esse é o charme da definição proposta agora. Ela não exige a real limpeza da órbita. Basta que o corpo tenha a capacidade de limpar sua órbita no tempo de vida do sistema planetário, mas não implica que isso tenha acontecido — permitindo que planetas co-orbitantes sejam definidos como planetas. 😉
Como diria o Chaves: Isso. Isso. Isso. 😉
Salvador, boa noite
O que quer dizer esse 1% dos exoplanetas que não passaram no teste? Ha outros objetos de porte semelhante em suas orbitas ou esse 1% são falsos positivos e esses planetas na verdade não existem?
Pelo que li, todos os planetas e candidatos (cerca de 5.000 objetos) para os quais havia estimativa de massa da estrela, massa ou diâmetro do planeta e órbita foram classificados e validados como planetas. Mas havia alguns poucos para os quais não havia esse trio de informações, e aí não foram verificados.
Se eu fosse Plutão estaria preocupadíssimo com essa classificação. Estou aqui sossegado na minha orbitazinha, e vem aqueles seres intrometidos, que nem sequer aprenderam as mínimas regras de convivência pacífica, a querer me classificar. Arre!!!
Bem, classificar é um bom modo de representar nosso nível de entendimento. Mas, claro, você tem razão, Plutão não está nem aí.
Salva, se o V774104, por estar no disco disperso, tiver uma órbita de baixíssima excentricidade, com o raio de Hills dentro do limite, sem nenhum outro objeto aparentando estar na mesma órbita, só faltaria ele ser esférico para ser um planeta… certo?
Ah, mas certamente tem um monte de objetos por ali. Só não os conhecemos, porque é difícil detectá-los. Mas há todo tipo de objeto do cinturão de Kuiper espalhado por aquelas excentricidades. E com essa nova definição, nem importa se há objetos lá e sim se o candidato em questão tem a capacidade de limpar sua órbita. Ter a órbita limpa só por estar vazia não vale. 😉
Pô… o rapaz nem teve trabalho para limpar a órbita e não pode ganhar o nome de planeta… sacanagem… hahahaha
Se Mercúrio orbitasse o Sol a mesma distância que Plutão orbita ou se Marte também estivesse a distância que Eris está, a divisão entre planeta e anões não seria muito clara.
É um bom argumento.
Olá, Salvador. Excelente matéria. Não obstante, tenho uma dúvida, que cai justamente nisso que o colega falou.
Não entendi porque a incapacidade de limpar a órbita é diretamente proporcional ao tamanho da faixa orbital do objeto.
Ou seja, quanto maior a órbita, quanto mais distante da estrela, maior precisa ser a massa do objeto para que ele seja considerado planeta.
Desde já, agradeço a resposta.
Gilmar, acredito que seja pela maior presença de planetesimais (a área a ser limpa é maior) nas órbitas mais externas. Ou seja, Mercúrio tem menos trabalho para limpar sua órbita pequena do que teria para limpar uma órbita maior, presumindo uma densidade similar de planetesimais presentes durante a formação do sistema planetário.
Exato, mas veja que de maneira inversa, mesmo o maior dos planetas anões teria dificuldades de limpar a sua região se estivesse na órbita de Mercúrio.
Perceba que as três linhas divisórias estão razoavelmente próximas: fiquei com a impressão que em qualquer sistema planetário suficientemente maduro dificilmente será encontrado um corpo muito próximo à essa faixa.
Não que não existam planetas/planetas-anões nessa região, mas quando os encontrarmos eles representariam uma quantidade tão pequena que não seriam o suficiente para derrubar essa metodologia.
É interessante observar também no diagrama que os planetas gigantes gasosos e os rochosos formam dois grupos distintos, o que mostra a importância do tamanho do planeta na “limpeza” da órbita.
Por se tratar de um trabalho de um americano eu ja imaginei que ele iria arrumar um jeito de encaixar plutão na definição da IAU de planeta, mas pelo visto a sensatez prevaleceu…
Acho que essa universidade de Los Angeles vai ter dificuldades de conseguir realizar trabalhos com a Nasa, onde estão os maiores interessados em elevar o status de Plutão! hehehe!
“Desacobertamentos” à parte, acho que a Nasa não faz esse tipo de preconceito, não. 😉
Salvador,
O resultado não poderia ser diferente, afinal, ele apenas construiu uma máquina ótica (neste caso matemática) para ratificar a produção do objeto planeta e por conseguinte do objeto não planeta. Em outras palavras, quando ele fez o trabalho, ele queria ratificar matematicamente a opção discursiva da IUA, não refutá-la é muito menos colocá-la em suspeição.
Em tempo… IAU
Carlos, concordo contigo. A surpresa não é que tudo tenha se encaixado em seu lugar. A surpresa é que exista um abismo tão grande entre planetas e planetas anões, como evidenciado no gráfico. Mostra que realmente há algo muito diferente entre as duas categorias de objetos. Se fosse apenas uma definição arbitrária a da IAU, Plutão poderia passar raspando de um lado, e Marte do outro. Mas há uma divisão clara, sem margem para controvérsia.
Muito interessante a matéria.
Uma coisa que eu gostaria que acontecesse é que fosse feita uma definição similar a essa para classificar Luas.
Em minha opinião asteroides que orbitam um planeta não deveriam ser classificados como luas, temos vários asteroides orbitando o sol e sobre essa definição oficial não são considerados planetas, o mesmo deveria ser válido para definir uma Lua, tanto que eles nem caem na categoria de ter massa o suficiente para ter o formato aproximadamente esférico, os cientistas deveriam criar uma nova categoria como Lua-anã ou Lua-asteroide para esses objetos.
Luas para mim são Europa, Ganimedes, Titan, etc tanto que ouvimos com frequência notícias sobre esses satélites, mas com que frequência temos notícias ou grande interesse nos asteroides que orbitam em torno Júpiter ou Saturno por exemplo?
É uma proposta interessante, de fato. É que a terminologia precisa é satélite, e satélite pode ser de qualquer tamanho. Até um Sputnik é um satélite — no caso, artificial! Mas concordo que seria uma boa distinguir entre luas e luas anãs, por assim dizer.
Proponho, luas-batatas or potato-moons!?
🙂
Marte perderia Fobos e Deimos. Plutão e Caronte, como definir?
Plutão seria planeta anão, e Caronte lua.
Salvador, imaginemos por um instante que Plutão e Netuno estivessem em rota de colisão, daria um belo espetáculo e traria consequências maiores pra nós aqui na terra?
Não, tudo muito longe de nós para nos preocupar. Mas seria uma pancada e tanto.
Salvador, boa tarde. Mesmo estando ambos planetas em órbitas externas da nossa Terra, não existe interação gravitacional importante, que naquele instante da colisão, influenciasse as trajetória dos outros planetas? Pequena que fosse mas com modificações de clima e até duração do tempo nos dias?
Não. Muito, muito longe.
Mas Salva, brincando ainda com isso. Vai que na colisão, caronte é arremessado para dentro do sistema, entra numa trajetória hiperbólica, e no final bate em alguém no caminho… surreal… o maior cometão de todos os tempos….
Caronte está a 20 mil km do centro de Plutão. Netuno tem uns 50 mil km de diâmetro. Se Plutão bater, Caronte também vai bater, provavelmente.
Esqueci, me perdoe: pela eliminação de massa no sistema a partir daquele instante?
Salvador, como são classificados “planetas” nômades, que não orbitam qualquer estrela?
O Margot diz que eles obviamente não se aplicam à definição, pois ela depende de o objeto estar orbitando em torno de uma estrela. E, se você for pensar, é mesmo complicado chamar de planeta algo que não orbita uma estrela — é como se o primeiro critério já fosse inválido. A ideia é chamar esses nômades de “free-floating objects”, ou objetos em flutuação livre.